O paradoxo do quadrado perdido
Origem: Wikipédia, a enciclopédia livre.
 |
| O Enigma do quadrado perdido |
 |
| O Enigma em animação |
Este arquivo é uma imagem em destaque na Wikipédia em inglês (Featured pictures) e é considerado uma das melhores imagens.
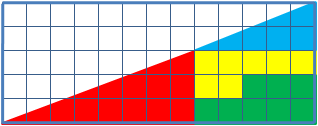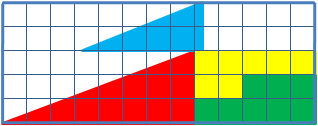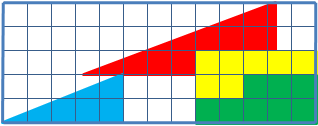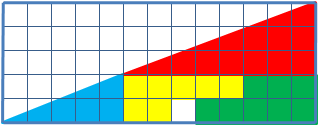
O paradoxo do quadrado perdido é um enigma resultado de uma ilusão de óptica, em que são vistos dois triângulos, formados pelas mesmas peças, onde porém um triângulo aparenta ter um pequeno quadrado a menos do que o outro. A suposta hipotenusa de cada figura não é reta (apesar de parecer).
De acordo com Martin Gardner, esse enigma foi elaborado em 1953 pelo mágico amador Paul Curry, de Nova Iorque. O enigma do quadrado perdido é por isso também chamado de paradoxo de Curry (embora exista o paradoxo de Curry de teoria ingênua dos conjuntos). O princípio por trás desse tipo de paradoxo é conhecido desde pelo menos 1860.
Explicação
Explicação
Antes da explicação, é necessário conhecer alguns conceitos básico de geometria com triângulos.
Triângulo
Origem: Wikipédia, a enciclopédia livre.
No plano, triângulo (também aceito como trilátero) é a figura geométrica que ocupa o espaço interno limitado por três linhas retas que concorrem, duas a duas, em três pontos diferentes formando três lados e três ângulos internos que somam 180°. Também se pode definir um triângulo em superfícies gerais. Nesse caso, são chamados de triângulos geodésicos e têm propriedades diferentes. Também podemos dizer que o triângulo é a união de três pontos não-colineares (pertencente a um plano, em decorrência da definição dos mesmos), por três segmentos de reta.
O triângulo é o único polígono que não possui diagonais e cada um de seus ângulos externos é suplementar do ângulo interno adjacente. O perímetro de um triângulo é a soma das medidas dos seus lados. Denomina-se a região interna de um triângulo de região convexa (curvado na face externa) e a região externa de região côncava (curvado na face interna).
Os Tipos De Triângulos
Os triângulos mais simples são classificados de acordo com os limites das proporções relativas de seus lados e de seus ângulos internos:
- Um triângulo equilátero possui todos os lados congruentes, ou seja, iguais. Um triângulo equilátero é também equiângulo: todos os seus ângulos internos são congruentes (medem 60°), sendo, portanto, classificado como um polígono regular.
 |
| Triângulo Equilátero |
- Um triângulo isósceles possui pelo menos dois lados de mesma medida e dois ângulos congruentes. O triângulo equilátero é, consequentemente, um caso especial de um triângulo isósceles, que apresenta não somente dois, mas todos os três lados iguais, assim como os ângulos, que medem todos 60º. Num triângulo isósceles, o ângulo formado pelos lados congruentes é chamado ângulo do vértice. Os demais ângulos denominam-se ângulos da base e são congruentes.
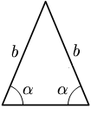 |
| Triângulo Isósceles |
Todos esses triângulos são os mesmos encontrados num plano de duas dimensões, porem em grandes extensões, como na superfície do planeta por exemplo, os ângulos para continuarem os mesmos é necessário que o comprimento dos lados sejam deformados ou seja ampliados em igual proporção ao perímetro da esfera.
- Um triângulo retângulo possui um ângulo reto. Num triângulo retângulo, denomina-se hipotenusa o lado oposto ao ângulo reto. Os demais lados chamam-se catetos. Os ângulos agudos de um triângulo retângulo são complementares (ou seja, sua soma é igual a 90°).
- Um triângulo obtusângulo possui um ângulo obtuso e dois ângulos agudos.
- Em um triângulo acutângulo, os três ângulos são agudos(formando 180°).

Condição de existência de um triângulo
Para que se possa construir um triângulo é necessário que a medida de qualquer um dos lados seja menor que a soma das medidas dos outros dois e maior que o valor absoluto da diferença entre essas medidas.

Fatos básicos
Fatos elementares sobre triângulos foram apresentados por Euclides nos livros 1-4 de sua obra Elementos aproximadamente em 300 a.C..
- Um triângulo é um polígono.
- Dois triângulos são ditos semelhantes se um pode ser obtido pela expansão uniforme do outro. Este é o caso se, e somente se, seus ângulos correspondentes são iguais, e isso ocorre, por exemplo, quando dois triângulos compartilham um ângulo e os lados opostos a esse ângulo são paralelos entre si. O fato crucial sobre triângulos similares é que os comprimentos de seus lados são proporcionais. Isto é, se o maior lado de um triângulo é duas vezes o maior lado do triângulo similar, diz-se, então, que o menor lado será também duas vezes maior que o menor lado do outro triângulo, e o comprimento do lado médio será duas vezes o valor do lado correspondente do outro triângulo. Assim, a razão do maior lado e o menor lado do primeiro triângulo será a mesma razão do maior lado e o menor lado do outro triângulo.
- Usando-se triângulos retângulos e o conceito de similaridade, as funções trigonométricas de seno e cosseno podem ser definidas. Essas são funções de um ângulo que são investigadas na trigonometria.
- Nos casos a seguir, será usado um triângulo com vértices A, B e C, ângulos α, β e γ e lados a, b e c. O lado a é oposto ao vértice A e ao ângulo α, o lado b é oposto ao vértice B e ao ângulo β e o lado c é oposto ao vértice C e ao ângulo γ.
- Na geometria Euclidiana, de acordo com o Teorema angular de Tales, a 32ª proposição de Euclides afirma que a soma dos ângulos internos de qualquer triângulo é igual a dois ângulos retos (180° ou π radianos). Isso permite a determinação da medida do terceiro ângulo, desde que sejam conhecidas as medidas dos outros dois ângulos. Por exemplo:
 |
| Triângulo 180º |
- Os ângulos A e A' são iguais (duas paralelas cortadas por uma transversal). Os ângulos B e B' são iguais por serem alternos internos. Os ângulos C e C' são iguais por serem opostos pelo vértice. Assim vê-se que a soma dos ângulos internos do triângulo é 180º.
- Existe um Corolário desse Teorema, que afirma que a medida de um ângulo externo de um triângulo é igual à soma das medidas dos ângulos internos não-adjacentes.
Ex: Sendo  a medida do ângulo externo do triângulo que tem como vértice o vértice
a medida do ângulo externo do triângulo que tem como vértice o vértice  pode-se afirmar que:
pode-se afirmar que: 
 a medida do ângulo externo do triângulo que tem como vértice o vértice
a medida do ângulo externo do triângulo que tem como vértice o vértice  pode-se afirmar que:
pode-se afirmar que: 
Um teorema central é o Teorema de Pitágoras, que afirma que em qualquer triângulo retângulo, o quadrado da medida da hipotenusa é igual à soma dos quadrados das medidas dos catetos. Se o vértice C do exemplo dado for um ângulo reto, pode-se escrever isso da seguinte maneira:
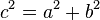
Isso significa que, conhecendo as medidas de dois lados de um triângulo retângulo, pode-se calcular a medida do terceiro lado — propriedade única dos triângulos retângulos.
O Teorema de Pitágoras pode ser generalizado pela lei dos cossenos:
Essa lei é válida para todos os triângulos, mesmo se γ não for um ângulo reto e pode ser usada para determinar o tamanho de lados e ângulos de um triângulo, desde que a medida de três ou dois lados e de um ângulo interno sejam conhecidas.
A lei dos senos diz:
onde d é o diâmetro da circunferência circunscrita ao triângulo (uma circunferência que passa pelos três vértices do triângulo). A lei dos senos pode ser usada para computar a medidas dos lados de um triângulo, desde que a medida de dois ângulos e de um lado sejam conhecidas.
Existem dois triângulos retângulos especiais que aparecem frequentemente em geometria. O chamado "triângulo 45º-45º-90º" possui ângulos com essas medidas e a proporção de seus lados é: 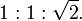
O "triângulo 30º-60º-90º" possui ângulos com essas medidas e a proporção de seus lados é:
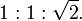
O "triângulo 30º-60º-90º" possui ângulos com essas medidas e a proporção de seus lados é:

Área do triângulo
Produto Base Altura
A área de um triângulo é a metade do produto da medida da sua altura pela medida da sua base. Assim, a área do triângulo pode ser calculada pela fórmula: onde h é a altura do triângulo, b a medida da base.
onde h é a altura do triângulo, b a medida da base.Triângulos equiláteros
Se o triângulo for equilátero de lado l, sua área A pode ser obtida com:
Ou então usando sua altura h e a fórmula da base vezes a altura. A altura h de um triângulo equilátero é:
Vale notar que essas duas fórmulas para os triângulos equiláteros são obtidas usando as funções seno ou cosseno e usando a altura do triângulo, que o divide ao meio em dois triângulos retângulos iguais.
De volta para a Explicação
 |
| Cunha Goed |
Descrição
Os dois triângulos formados por peças coloridas parecem ter a mesma área de 13 quadradinhos (base) x 5 quadradinhos (altura) : 2 (ou x 1/2):

As peças de cada triângulo formado por peças:
- Um triângulo (aqui azul) com área de 5 quadradinhos (base) x 2 quadradinhos (altura) : 2 (ou x 1/2):

Outro triângulo (aqui vermelho) com área de 8 quadradinhos (base) x 3 quadradinhos (altura) : 2 (ou x 1/2):

- Duas outras figuras (aqui, uma laranja e a outra verde), que juntas tem o tamanho de um retângulo com um lado com 5 quadradinhos e o outro lado com 3 quadradinhos
- a área do retângulo é obtida multiplicando a largura pela altura.
- área que é a soma deda figura amarela
da figura verde
Embora ambos sejam visualmente triângulos de mesmo tamanho com sub-áreas idênticas, no segundo triângulo há um quadrado de área  restando.
restando.
 restando.
restando.Solução
A soma das áreas das peças resulta em uma área de 
No entanto, um triângulo com lados 13 e 5 deve ter uma área de
Assim, está dada a prova matemática de que o dado triângulo não pode ser formado por essas peças.
O paradoxo se deve a diferença entre os ângulos dos triângulos azul e vermelho (eles não são triângulos similares). Portanto, a hipotenusa não é uma reta. Matematicamente, isso pode ser provado da seguinte maneira:
- Triângulo azul:

- Triângulo vermelho:

- Ângulo de um triângulo com catetos 13 e 5:

Disso percebe-se que o lado de cima não é uma linha reta. Portanto, a figura composta não é realmente um triângulo, mas sim um quadrilátero.
Figuras enganosas como essa podem também ser formadas com outras proporções. As dimensões inteiras dos lados das figuras de cima: 2, 3, 5, 8 e 13; são cinco números consecutivos da sequência de Fibonacci. Muitas outras figuras, que apresentam o mesmo fenômeno, também são feitas com outros números consecutivos na sequência de Fibonacci.
Figuras enganosas como essa podem também ser formadas com outras proporções. As dimensões inteiras dos lados das figuras de cima: 2, 3, 5, 8 e 13; são cinco números consecutivos da sequência de Fibonacci. Muitas outras figuras, que apresentam o mesmo fenômeno, também são feitas com outros números consecutivos na sequência de Fibonacci.
Seqüência de Fibonacci
A sequência tem o nome do matemático pisano do século XIII Leonardo de Pisa, conhecido como Leonardo Fibonacci, e os termos da sequência são chamados números de Fibonacci. Os números de Fibonacci são, portanto, os números que compõem a seguinte sequência de números inteiros:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …
Com esta fórmula podemos montar a sequência de Fibonacci:
 |
| Blocos de Fibonacci |
Fontes:
http://pt.wikipedia.org/wiki/Paradoxo_do_quadrado_perdido
https://pt.wikipedia.org/wiki/Tri%C3%A2ngulo
http://pt.wikipedia.org/wiki/N%C3%BAmero_de_Fibonacci

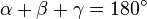



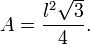
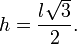



Nenhum comentário:
Postar um comentário